로그변환과 np.log()가 아닌 np.log1p()를 하는 이유

1.로그변환의 이유

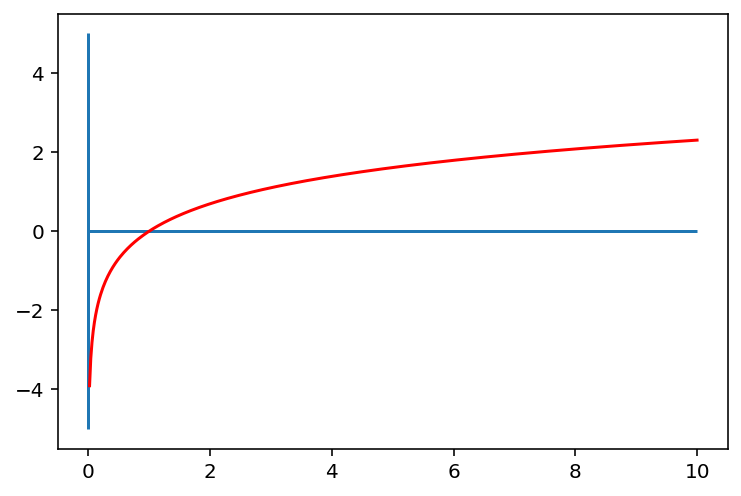
위와 같은 로그 함수의 특징은 다음과 같습니다.

• \(0< x <1\) 범위에서는 기울기가 매우 가파릅니다.
  즉, \(x\)의 구간은 \((0,1)\)로 매우 짧은 반면, \(y\)의 구간은 \((-∞,0)\)으로 매우 큽니다.

• 따라서 \(0\)에 가깝게 모여있는 값들이 \(x\)로 입력되면, 그 함수값인 \(y\) 값들은 매우 큰 범위로 벌어지게 됩니다.
  즉, 로그함수는 \(0\)에 가까운 값들이 조밀하게 모여있는 입력값을 넓은 범위로 펼칠 수 있는 특징을 가집니다.

• 반면, \(x\)값이 점점 커짐에 따라 로그함수의 기울기는 급격히 작아집니다.
  이는 곧 큰 \(x\)값들에 대해서는 \(y\)값이 크게 차이나지 않게 된다는 뜻이고 이에 따라서 넓은 범위를 가지는 \(x\)를 비교적 작은 \(y\)값의 구간 내에 모이게 하는 특징을 가집니다.

• 그렇기에 결과적으로 데이터의 분포를 모았을 때 밀집되어 있는 부분은 퍼지게
  퍼져있는 부분은 모아지게 만들 수 있는 것입니다.

위와 같은 특성 때문에 한 쪽으로 몰려있는 분포에 로그 변환을 취하게 되면 넓게 퍼질 수 있는 것이죠.

왜 한쪽으로 치우친 분포를 로그 변환을 취하게 되면 정규분포 모양으로 고르게 분포하게 될 수 있는지 이해가되었으면 왜 numpy 로그변환에서 np.log()가 아닌 np.log1()을 사용하는 이유에 대해 알아보겠습니다.

2. np.log()가 아닌 np.log1p()인 이유

로그함수의 경우 위의 자연로그 함수 그래프를 보면 알겠지만, \(x = 0\) 인 경우 \(y\)가 -무한대(-infinite)의 값을 가집니다.
아래의 Out[2]번에 보면 NumPy 에 \(0\)이 포함된 배열을 np.log() 함수에 대입하면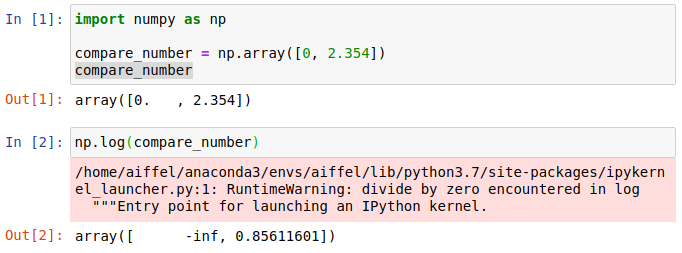

‘RuntimeWarning: divide by zero encountered in log’ 라는 경고메시지가 뜨고, -inf 가 포함된 배열을 반환하게 됩니다. \(x\)가 \(0\)의 값을 가지면 무한대가 되므로 당연한 결과입니다. 이를 해결하기 위한 방법으로 \(x + 1\)을 해줘서
\(0\) \(1\) 으로 바꿔주면 문제가 없게 됩니다. np.log1p() 함수가 바로 이 역할을 해주는 함수입니다.
그러면 \(y\)값이 -inf⇒ \(0\)으로 바뀌게 되죠. 마찬가지의 방법으로 np.log(1+값)을 해주면 np.log1p()와 같은 값을 얻을 수 있습니다.

np.log1p()	np.log(1+값)

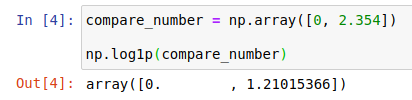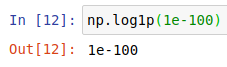
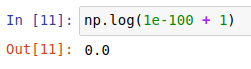
하지만 변환 전의 값이 너무 작은 경우 컴퓨터 계산의 오류가 생기기 때문에 직접 \(+1\) 을 해주는 것이 아닌 np.log1p()을 사용하는 습관을 들이는 게 좋을 것입니다.

np.log1p()	np.log(1+값)